Pembahasan Fungsi Invers
Dalam sistem pencatatan penduduk kini diterapkan Nomor Induk Kependudukan (NIK). Nomor ini merujuk pada data tercatatnya seseorang sebagai penduduk Indonesia. Dalam lingkup lebih sederhana, misalkan di sekolah. Masing masing siswa diberi Nomor Induk Siswa atau NIS. Hubungan antara pemilik nomor NIK/NIS tersebut dengan nomor yang dimilikinya disebut sebagai korelasi khusus yang diistilahkan dengan fungsi.Lalu bagaimana kalau ditinjau secara terbalik “ korelasi antara nomor NIK/NIS dengan pemiliknya”. Peninjauan terbalik ini yang disebut dalam matematika sebagai fungsi invers. Lebih lanjut mengenai fungsi invers ini dijelaskan sebagai berikut.
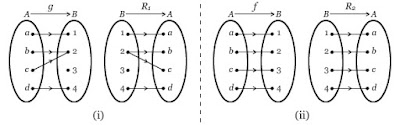
Bila fungsi g dibalik maka akan didapatkan korelasi R1. Relasi R1 ini yang disebut invers (kebalikn) dari fungsi g. Lalu pertanyaan selanjutnya apakah R1 tersebut fungsi? Senada dengan g (x) Perhatikanjuga pada fungsi f f: A->B pada bab gambar ii. Jika fungsi dibalik maka didapat korelasi R2. Dan apakah R2 ini sebuah fungsi juga?
Pada fungsi g, invers g yang mempunyai korelasi R1. Maka ada anggota B (domain) tidak mempunyai pasangan di kawasan kodomai. Artinya pada fungsi g , invers g yang dinyatakan dengan R1 bukan merupakan sebuah fungsi invers. Dengan kata lain g(x) tidak mempunyai fungsi invers.
Sekarang lanjut pada fungsi f. Invers f yang mempunyai korelasi R2. Terlihat gotong royong mereka mempunyai sempurna satu pasangan atau dalam istilah matematika korespondensi satu satu. Karena ini memenuhi syarat sebuah korelasi dikatakan fungsi maka R2 ialah fungsi, dengan kata lain fungsi f mempunyai fungsi invers.
Dari penyelesaian di atas didapat gotong royong setiap fungsi kalau dikomposisikan dengan fungsi inversnya akan kembali ke domain. Sifat ini dikenal dengan identitas. Kesimpulannya antara fungsi dan fungsi invers akan menciptakan identitas dikala di komposisikan. Sumber http://www.marthamatika.com/
Syarat Fungsi Invers
Sebelum dijelaskan lebih lanjut, perhatikan gambar (i) dibawah ini. Fungsi g(x) mendefenisikan g: A-> B.Bila fungsi g dibalik maka akan didapatkan korelasi R1. Relasi R1 ini yang disebut invers (kebalikn) dari fungsi g. Lalu pertanyaan selanjutnya apakah R1 tersebut fungsi? Senada dengan g (x) Perhatikanjuga pada fungsi f f: A->B pada bab gambar ii. Jika fungsi dibalik maka didapat korelasi R2. Dan apakah R2 ini sebuah fungsi juga?
Pada fungsi g, invers g yang mempunyai korelasi R1. Maka ada anggota B (domain) tidak mempunyai pasangan di kawasan kodomai. Artinya pada fungsi g , invers g yang dinyatakan dengan R1 bukan merupakan sebuah fungsi invers. Dengan kata lain g(x) tidak mempunyai fungsi invers.
Sekarang lanjut pada fungsi f. Invers f yang mempunyai korelasi R2. Terlihat gotong royong mereka mempunyai sempurna satu pasangan atau dalam istilah matematika korespondensi satu satu. Karena ini memenuhi syarat sebuah korelasi dikatakan fungsi maka R2 ialah fungsi, dengan kata lain fungsi f mempunyai fungsi invers.
Sebuah korelasi dikatakan fungsi kalau semua domain mempunyai lawan di kawasan kodomain. Agar gampang meningat misalkan kawasan Domain Wanita Cantik, dan Kodomain ialah lelaki. Ingat perempuan anggun tidak ada yang jomblo.Dari proses di atas hendaknya sanggup disimpulkan perbedaan invers fungsi dan fungsi invers. Ingat: Setiap fungsi mempunyai invers fungsi, tetapi tidak semua fungsi mempunyai fungsi invers. Selanjutnya akan dilihat teladan soal dan pembahasan wacana fungsi invers.
Contoh Soal dan Pembahasan Fungsi Invers
Dari diagram di atas apakah f-1 ada? Jelaskan alasannya. Kemudian carilah (f-1 o f) (x) , (f-1 of) (y) dan (f-1 o f)(z). Apa kesimpulan yang sanggup diperoleh?
Dari gambar di atas f-1 dan f merupakan korespondensi satu satu. Bisa dikatakan f mempunyai fungsi invers.
f-1 o f (x) = f-1 (f(x) = f-1 (c) = x. Untuk f-1 o f (y) = f-1 (f(y) = f-1 (a) = y. Dan untuk f-1 o f (z) = f-1 (f(z) = f-1 (b) = z.

Post a Comment for "Pembahasan Fungsi Invers"