Rumus Memilih Besar Dan Arah Resultan Vektor Beserta Teladan Soal Dan Pembahasannya
Dalam artikel tentang cara melukiskan vektor resultan dengan metode grafis sudah dibahas secara detail tentang bagaimana cara memilih resultan vektor dengan metode segitiga, jajargenjang dan poligon. Namun ketiga metode dalam artikel tersebut spesialuntuk dipakai untuk melukiskan vektor resultan saja, sehingga nilai dan arah resultan spesialuntuk sanggup ditentukan dengan proses pengukuran.
Nah dalam artikel ini akan dibahas, cara simpel memilih besar dan arah resultan vektor dengan melalui proses perhitungan yaitu dengan menggunakan Rumus Cosinus-Sinus. Lalu menyerupai apa rumus cosinus-sinus tersebut? Untuk memahami rumus cosinus-sinus, perhatikan klarifikasi diberikut ini.
Penurunan Rumus Cosinus-Sinus
Sebenarnya, rumus cosinus-sinus diperoleh dengan memakai asas trigonometri atau lebih tepatnya Dalil Pythagoras pada metode Jajargenjang, sehingga penentuan besar dan arah vektor resultan dengan rumus cosinus-sinus ini sanggup dikatakan cara memilih besar dan arah vektor resultan dengan memakai metode jajargenjang.
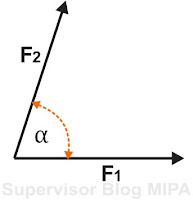
Untuk penurunan rumus cosinus-sinus, perhatikan gambar vektor gaya F1 dn F2 yang bekerja pada satu titik membentuk sudut sebesar α diberikut ini.
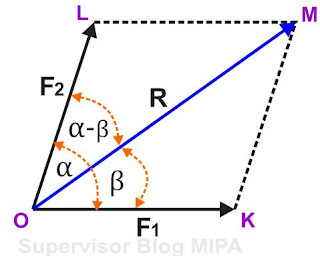
Dari gambar dua vektor F1 dn F2 yang membentuk sudut α di atas, maka dengan memakai metode jajar genjang, vektor resultan R dapat dilukiskan menyerupai pada gambar diberikut ini
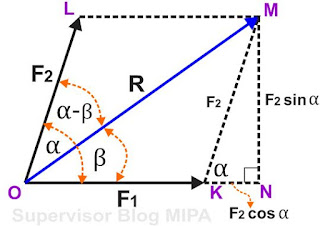
melaluiataubersamaini adanya vektor resultan R, maka terbentuk dua sudut baru, yaitu sudut antara R dengan F1 (β) dan sudut antara R dengan F2 (α- β). Dari berdiri jajargenjang OKML, perhatikan gambar segitiga OKM. Jika kita tarik garis perpantidakboleh dari OK ke kanan, maka akan terbentuk segitiga siku-siku KNM, menyerupai pada gambar diberikut ini.
melaluiataubersamaini memakai rumus trigonometri, maka diperoleh hasil menyerupai diberikut:
KM | = F2 |
KN | = F2 cos α……………….(pers. 1) |
NM | = F2 sin α………………..(pers. 2) |
Perhatikan gambar segitiga ONM, segitiga ini ialah segitiga siku-siku sehingga berlaku Hukum Pythagoras sebagai diberikut
(OM)2 | = (ON)2 + (NM)2 |
(OM)2 | = (OK + KN)2 + (NM)2 ………………(pers. 3) |
Dari gambar jajargenjang OKML, kita sanggup mengetahui bahwa:
OM | = R dan OK = F1..................................(pers. 4) |
Jika persamaan 1,2 dan 4 disubtitusikan ke persamaan 3, maka akan menghasilkan persamaan sebagai diberikut:
R2 | = (F1 + F2 cos α)2 + (F2 sin α)2 |
R2 | = F12 + 2 F1F2 cos α + F22 cos2 α + F22 sin2 α |
R2 | = F12 + F22 (sin2 α + cos2 α) + 2 F1F2 cos α………(pers. 5) |
Kita tahu bahwa nilai dari sin2 α + cos2 α = 1, maka persamaan 5 menjadi
R2 | = F12 + F22 + 2 F1F2 cos α…………….(pers. 6) |
Dari persamaan 6, maka rumus final untuk menentukan besar vektor resultan atau kita sebut sebagai Rumus Kosinus adalah sebagai diberikut:
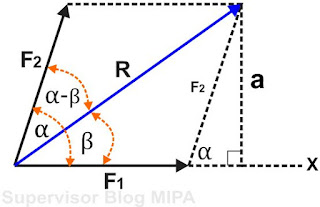
Sesudah rumus untuk memilih besar vektor resultan sudah diketahui, lalu bagaimana rumus untuk memilih arah vektor resultan? Untuk menjawaban pertanyaan tersebut, perhatikan gambar di bawah ini
Dari gambar di atas, sudut α adalah sudut yang dibuat vektor F2 terhadap F1 dan sudut β adalah sudut yang dibuat vektor R terhadap F1, dan garis X ialah garis perpantidakboleh dari gari vektor F1 yang tegak lurus terhadap garis a, dengan memakai rumus sinus kita peroleh
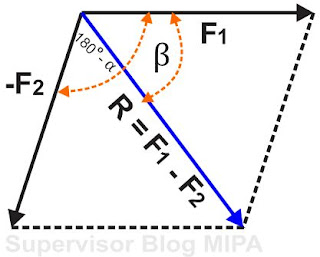
Persamaan 11 di atas ialah rumus hubungan antara vektor F2 dengan vektor R. Selanjutnya kita akan memilih rumus hubungan antara vektor F1 dengan vektor R. Untuk itu perhatikan gambar diberikut ini.
Dari gambar di atas, sudut α adalah sudut yang dibuat vektor F1 terhadap F2 dan sudut (α –β) adalah sudut yang dibuat vektor R terhadap F2, dan garis Y ialah garis perpantidakboleh dari gari vektor F2 yang tegak lurus terhadap garis b, dengan memakai rumus sinus kita peroleh
Jika persamaan 12 kita bagi dengan persamaan 13, maka akan diperoleh
Persamaan 14 sanggup kita tuliskan menjadi menyerupai ini
Jika persamaan 11 dan 15 kita gabung maka akan menghasilkan rumus untuk menentukan arah vektor resultan atau kita sebut sebagai Rumus Sinus yaitu sebagai diberikut
Teknik Menentukan Besar dan Arah Vektor Resultan dengan Rumus Cosinus-Sinus
Misalkan terdapat soal menyerupai ini
Dua buah vektor F1 dan F2 masing-masing besarnya 4 N dan 5 N dan mempunyai titik awal berhimpit. Hitunglah nilai dari F1 + F2-dan F1 – F2 serta tentukan arah resultan vektornya bila sudut apit antara kedua vektor tersebut ialah 60o.
Penjumlahan Vektor dengan Rumus Cosinus-Sinus
Dari soal di atas, resultan dari F1 + F2 dapat digambarkan menyerupai ini
melaluiataubersamaini memakai rumus cosinus, besar resultannya adalah
R | = √(|F1|2 + |F2|2 + 2 |F1| |F2| cos α) |
R | = √(42+ 52 + 2. 4. 5. cos 60) |
R | = √(16+ 25 + 40. 0,5) |
R | = √(41 + 20) |
R | = √61 = 7,81 N |
melaluiataubersamaini memakai rumus sinus, arah resultannya adalah
R/sin α | = F2/sin β |
sin β | = (F2/R). sin α |
sin β | = (5/7,81). sin 60 |
sin β | = 0,64. 0,87 |
sin β | = 0,5568 |
β | = arc sin (0,5568) = 33,83o |
Pengurangan Vektor dengan Rumus Cosinus-Sinus
Dari soal di atas, resultan dari F1 - F2 dapat digambarkan menyerupai ini
melaluiataubersamaini memakai rumus cosinus, besar resultannya adalah
R | = √(|F1|2 + |F2|2 + 2 |F1| |F2| cos (180-α) |
R | = √(|F1|2 + |F2|2 + 2 |F1| |F2|.- cos α) |
R | = √(|F1|2 + |F2|2 - 2 |F1| |F2| cos α) |
R | = √(42 + 52 - 2. 4. 5. cos 60) |
R | = √(16+ 25 - 40. 0,5) |
R | = √(41 - 20) |
R | = √21= 4,58 N |
melaluiataubersamaini memakai rumus sinus, arah resultannya adalah
R/sin (180-α) | = F2/sin β |
sin β | = (F2/R). sin (180 – α) |
sin β | = (F2/R). sin α |
sin β | = (-5/7,81). sin 60o |
sin β | = -0,64. 0,87 |
sin β | = -0,5568 |
β | = arc sin (-0,5568) = - 33,83o |
Demikianlah artikel tentang cara cepat memilih besar dan arah vektor resultan dengan memakai rumus kosinus-sinus. Semoga sanggup bermanfaa untuk Anda. Terimakasih atas kunjungannya dan hingga jumpa di artikel diberikutnya.
Sumber https://www.fisikabc.com/




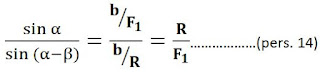


Post a Comment for "Rumus Memilih Besar Dan Arah Resultan Vektor Beserta Teladan Soal Dan Pembahasannya"